Home > Controversy on Authorship > The Possible Authors > José Clemente Orozco
José Clemente Orozco is the third person identified as a possible author of the project for the Home-and-Studio at López Cotilla. With the purpose of evaluating the probability of famed muralist being, in fact, the author of the project, a brief review of dates relevant to the topic was made; mentions and testimonies crediting him with the authorship were analyzed; and a retelling of the motivations and circumstances that allowed the realization of the Home-and-Studio was made. In addition, his approach to architecture and its presence in his pictorial works was studied; and finally, the relationship between dynamic symmetry and his work, and the project at hand was dealt with at depth. The understanding of the listed variables will allow the evaluation of Orozco’s degree of involvement in the project’s realization.
As to the dates, in the present research, the coincidence in the times of elaboration and execution of the project with the place of residence of the possible authors has taken relevance, and even though there is acknowledgement to the fact that this is may not be a determinant factor, it is information worth taking into account. For the ends of this section, it suffices to mention that the dates are completely favorable to Orozco. Since, both during the time of the project’s elaboration (second semester of 1936) and the time of construction of the Home-and-Studio (end of 1936 to the first trimester of 1938), Orozco lived permanently in the city of Guadalajara. This would have allowed him to take over the project and construction personally.
About the testimonies on who elaborated the project for the Home-and-Studio, it is relevant that Orozco is the only one of the three listed possible authors that openly pronounced himself as the project’s author. There are no similar statements from Rafael Urzúa nor Luis Barragán. This takes a great significance, because an artist with the prestige, renown and cultural influence of José Clemente Orozco would not take credit for a work that did not belong to him.
Regarding the circumstances and Orozco’s motivations to take upon the construction of his Home-and-Studio of López Cotilla, if the brief period of time he occupied it (less than two years) is considered, and contrasted with the enormous effort it meant to build it, the reasons why the famed muralist decided to take upon its construction are not immediately clear.
According to some authors, the painter had planned to stay in Guadalajara, since he enjoyed its climate and tranquility. Regardless that Orozco was, indeed, partial to this city, these versions have little credibility in the light of the following facts:
– The Home-and-Studio was designed as a temporary Workshop-Dormitory for the painter, since the architectural program did not include bedrooms for his children (Clemente, Alfredo and Lucrecia). As far as the available information allows, the Orozco-Valladares family remained in Mexico City during the elaboration of the three murals in Guadalajara. It was only during school vacations that the family came to Guadalajara to visit their father and husband.
– Orozco acquired the plots of López Cotilla St in Guadalajara and of Ignacio Mariscal St in Mexico City practically and the same time, being the latter where he did plan to live with his family. This can be deduced from a letter sent to his wife, Doña Margarita Valladares, dated on November 11, 1937 (a few months before he moved into the Home-and-Studio at López Cotilla St), in which he expresses, amongst other things, the following:
… I have thought that the best is to make a home for the family at the plot there [Ignacio Mariscal] instead of just a studio. That can be on the 2° floor, with a completely independent entrance. Once I get through this, we can take on the building there. Let us see if you can occupy it with the children by the second semester of the year. Four bedrooms and three bathrooms can be built very well, in addition to the services and the studio. You will see…1
Why then, did he take on building the Home-and-Studio at López Cotilla St? Based on the available information, the following hypothesis was formulated:
Orozco had imagined, for many years, his “Ideal-Studio”, a space designed especially with the purpose of carrying out his small-scale oeuvre (painting, engraving and drawing). On this particular point, it is convenient to review the following passage by Alma Reed regarding a birthday present that the painter received during his stay in New York from his mother, Mrs. Rosa Flores:
One of those anniversaries, I remember, his present was a cheerful picture (painted by her) on silk, of a house, tall and with wide windows, with the Mexican sun throwing its rays at it, and palm trees beautifying both sides of the entrance. It was labelled with a precise and well-formed label: “My son’s ideal studio” 22
His stay in Guadalajara (from 1935 to 1939) presented a unique opportunity for the famed muralist to finally “build” his “Ideal-Studio”. Several motivations and circumstances aligned to make this possible.
– Since his arrival to Guadalajara and until he occupied his Home-and-Studio, Orozco did not count with a space where he could work on his smaller-scale oeuvre, limiting him to the works of mural painting. Orozco himself mentions this in a letter sent to the art promotor Inés Amor, dated on January 20, 1938, where he explains the following:
...Until now, I have only been doing the work of the walls [murals], since I did not count with an appropriate studio to make small paintings, and, on that account, I had the idea to take on the construction of said studio [López Cotilla], which is practically finished. Next week I will occupy and be able to use it…3
In a later letter, dated on December 18, 1948, directed to don Justino Fernández, the muralist underlines the importance that it meant to him to count with an adequate space for painting:
... for the vault studios, as for the other works that the governor wants, a studio is necessary, and since there are none in Guadalajara, it must be built, like last time I had to build the one of López Cotilla, which I had to sell. In a room of a common house, it is impossible to make a painting of any importance. It is, simply, a matter of need. 4 4
For Orozco, a space apt for the production of his small-scale work was essential. The need of having an ideal place to work on his smaller-scale oeuvre at his disposal, and not being limited only to mural painting was the main motivation of the construction of the Home-and-Studio at López Cotilla St.
– By recommendation of architect Luis Barragán, he acquired, with certain facilities, a plot with the required orientation (North-South) for his new studio, located at the newly inaugurated urbanization that was developed on the grounds of the Ex-Penitentiary of Escobedo, very close to the city center and to the buildings where he was to paint the three mentioned murals.
– His permanent stay in the city of Guadalajara allowed him to participate in a direct manner in the elaboration of the architectural project of his Home-and-Studio, which, in addition to fulfilling the spatial and functional requirements dictated by him, should also express his very particular vision on the formal aspect of the building.
– For the realization of this adventure, Orozco counted with the support of two local characters who would turn out fundamental to the project’s completion.
In the first place, his young friend Luis Barragán, who, along with his brother Juan José, had just concluded in the same area the design and construction of the Revolution Park, in addition of carrying out, on the blocks neighboring the park, the construction of several houses for rent and sale.
In the second place, the also young Jaliscience engineer Rafael Urzúa, who surely met Orozco through Barragán. He also had personal contact with the renowned muralist, since, as head of the Section of Construction and Architecture of the office of Public Works of the H. Municipality of Guadalajara, he was responsible for rehabilitating the dome of the present-day Hall of the University to prepare it for the realization of mural painting.
Orozco and Urzúa had at least two other common acquaintances: in the first place, painter León Muñiz, who was the muralist’s helper and a close friend of Urzúa’s, who designed his home on 1390 De La Paz Ave. In the second place, engineer Heliodoro Rojas, who was a schoolmate of Urzúa at the School of Engineering, and was responsible on the behalf of the State Government of hiring the artist.
Both Barragán and Urzúa participated in the real estate boom that detonated in this area of the city. Both experts carried out an intense professional activity, including both design and construction, of various buildings, and counted with a solid network of providers and work personal which they surely put at Orozco’s disposal when he took on the construction of his Home-and-Studio.
– The construction of his Home-and-Studio also represented the opportunity to turn his very particular and advanced view on Mexican architecture into a reality, as well as the opportunity to incorporate the concepts on modern architecture assimilated during the frequent talks in New York City with his friend, the prestigious Viennese architect Frederick Kiesler.
Orozco introduced Kiesler to Luis Barragán, and several authors have documented that, during Barragán’s stay in New York in 1931, he participated, on Orozco’s invitation, in several of these talks on modern architecture.
– It is likely that, by the time Orozco arrived to Guadalajara on 1935, he knew about or even had visited the home and studio that architect Juan O’Gorman designed and built from 1931 to 1932 for his friends, the painters Diego Rivera and Frida Kahlo. The home and studio is located on Las Palmas St (present-day Diego Rivera St), corner with Altavista St, in Colonia San Ángel Inn, in Mexico City.
This, doubtlessly, could have been an additional motivation for the Jaliscience muralist to decide on building his Home-and-Studio on López Cotilla St, since he could then contrast the functionalist project, with a strong Corbusian influence, of the O’Gorman-Rivera pair with the modern and abstract one carried out by the Barragán-Orozco dyad, more influenced by Kiesler and Loos.

Fig. 1. Sketch of the Diego Rivera Home and Studio, by Juan O’Gorman.
https://estudiodiegorivera.inba.gob.mx/2014-01-20-19-04-02/historia.html
Orozco had many connections with architecture throughout his life. These go back to his education at the National School of Agriculture and Veterinary form 1898 to 1901, where he acquired his first knowledge of Geography and Topography, as well as Geometry, perspective and technical drawing5. Later, he entered the National Preparatory School with the vague intention of studying architecture6. He remained at this School for four years, where he carried out studies that qualified him as an architect’s assistant7. After the passing of his father, Orozco even worked as a draftsman at the firm of architect Carlos Herrera8.
Orozco quits his intention of becoming an architect in 1904, following the accident where he lost his left hand. From this moment on, he decides on dedicating himself to his true passion: painting. However, he never lost interest in architecture, which emerges constantly in his works, and even shapes it.
Orozco’s knowledge on architecture would turn out crucial for the development of his murals, in which he makes and extraordinary fusion of both arts. José Clemente Orozco’s mastery of architecture was widely recognized by Frank Lloyd Wright, who, referring to the mural at the New School for Social Research makes a dissertation on the relationship between painting and architecture in Orozco’s oeuvre:
The fresco is not only a mural, but also something integral. Therefore, basic knowledge of architecture is essential. […] The difference between a fresco and other kinds of painting lies fundamentally in the fact that the fresco is part of the construction itself, an integral part of its flesh, from which the building is truly impregnated with color, which leads to architecture to a higher imagery, obviated from what reasonably belongs to the architect.
However, and at the same time, the fresco of mural painting must part from architecture [...] But I believe that nothing worth noting will happen as great art, until the architect is an expert in frescos, and the fresco painter masters architecture. […] 9
Orozco, throughout his life, related both professionally and personally with renowned architects, amongst which, stand out Joseph Urban and Frank Lloyd Wright, whom, along with Frederick Kiesler, he met it New York. This went as far as Lloyd Wright inviting Orozco as a professor to his school of art and architecture known as Taliesin. Orozco rejected this proposal11. In Guadalajara, he held friendships with members of the Tapatía School of Architecture. This includes the already mentioned architects Rafael Urzúa, Luis Barragán and Ignacio Díaz Morales. Likewise, he held a professional relationship and friendship with Mario Pani, who invited him to paint two murals on buildings of his authorship 11, 12.

Fig. 2. Orozco working on the mural La Primavera (Spring), at the Presidente Alemán urban complex, by architect Mario Pani. Mario Pani Darqui Facebook page.
https://www.facebook.com/45333513433/posts/10154895706928434/?substory_index=0&app=fbl
Orozco always recognized the important and close relationship between painting and architecture. Below is a transcript of a part of the article, covered by the El Informador de Guadalajara journal, of the conference given by him in 1949 at the Faculty of Architecture of the University of Guadalajara, on architect Ignacio Díaz Morales’s invitation.
… [Orozco] spoke of the close relationships that exist between the plastic arts, but he stated that these relationships are even more precise between painting and architecture, underlining the different times when the problem of this relationship has best been solved. Regarding this, he discussed, with his characteristic humility, the great pictorial-architectonic work executed at the chapel of the Cabañas Hospice […] 13
A relevant fact regarding the relationship of Orozco with architecture is that, in 1943, the Sociedad de Arquitectos Mexicanos (Society of Mexican Architects) granted him the title of honorary member, recognizing, with this, the contributions of his pictorial work to the area of architecture. 14

Fig. 3. Document granting Orozco the title of honorary member of the Sociedad de Arquitectos Mexicanos, 1943.
Orozco, Verdad Cronológica. Clemente Orozco Valladares.
In his book, México en la obra de Octavio Paz (Mexico in the work of Octavio Paz), in the third title Los privilegios de la vista (The privileges of sight), the Nobel Prize in Literature laureate refers in the following manner to Orozco’s relationship to architecture:
In his visions of Mexico, sometimes white, gray, ochre cubes appear; they are houses from which mourning women, funeral processions exit. In other occasions, he paints panoramas of domes, churches, towers, forts, walls, terraces: what is left of ancient Mexico. These backdrops are painted with nostalgia, and are as a goodbye to a disappeared word. I add that all of these urban landscapes are built; I mean: the eye and the hand of Orozco are architects. He was a great painter of volumes and solids. He was an inspired, but also, a geometrician. 15
An essential character in the development of Orozco’s ideas regarding architecture was the Austrian architect Frederick Kiesler. Orozco begins a friendship with hip in New York City, where Orozco arrived in 1927. Kiesler was, in a great measure, responsible for the diffusion of European modernist and avant-garde ideas in the new continent.
Through him, Orozco gets to know the ideas of another modern architect Adolf Loos. Loos positions himself against any ornament in architect, explaining that cultural evolution is equivalent to the elimination of ornament in the usual object16. As mentioned in the previous section, Orozco and Kiesler used to hold talks about modern architecture, in which they surely shared and developed ideas on architectural abstraction.
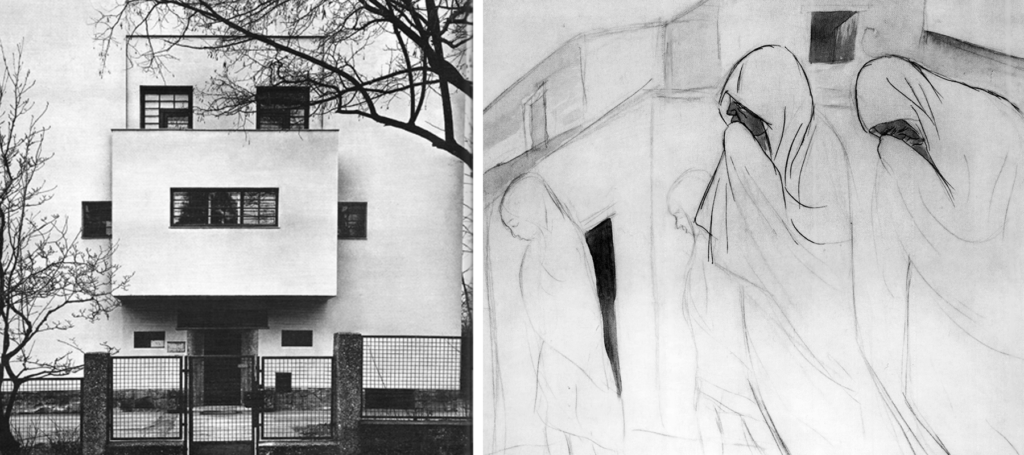
Fig. 4. Villa Müller (1933) https://sancheztaffurarquitecto.wordpress.com/2008/09/20/adolf-loos-1870-1933/
Fig. 5. Lágrimas (Tears) (1926-28) Colección INBA/MACG.
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes and Beatriz Eugenia Mackenzie.
Both on his murals as on his small-scale work, architecture is constantly present in Orozco’s works. His particular vision on how Mexican architecture ought to be can be observed since the 20s decade of last century, both in the murals of the National Preparatory School as on his famous oil painting The White House, made circa. 1922. In some of his works, architecture serves as framework for the happenings of human activity, while in others, it is not limited to be a stage, but rather, becomes the protagonist of the composition.

Fig. 6. Murals at the National Preparatory School known as Workers and The Farewell. Note the architectural volumes in the background, particularly, the leap of heights on the wall on the left side.
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes y Beatriz Eugenia Mackenzie.

Fig. 7. La Despedida (1928) Colección INBA/MACG.
Fig. 8. El Fusilado (The shot man) (1926-28) Colección INBA/MACG. Architecture as a stage.
In a great deal of his works, Orozco carries out exercises of abstraction of Mexican architecture, bringing it down to its most simple and pure shapes. Out of these exercises, the picture called La Casa Blanca (The White House) (oil paint on canvas 64x76)17 painted in Mexico City between 1922 and 1925 stands out for its influence. This was one of the five paintings that he brought to his trip to New York (1927 to 1934) as a sample of his work.

Fig. 9. The White House (1922-25) Colección INBA/MACG.
The “white cube” as abstraction of architecture.
A lonely landscape in chiaroscuro, a leafless tree on arid soil, and three silhouettes that seem to leave, scared, are the frame of a lonely dwelling, represented by a white cube, seen in perspective, a clean white volume, with flat ceilings, lacking windows, with its sobriety only interrupted by the doorframe. The project of an austere, honest, modern and Mexican architecture.
The picture of this enigmatic white cube was present for many years in Orozco’s mind and work. It appears in many of his works, especially in the graphic work he carried out during his stay in New York, from 1927 to 1934. This white cub was even the base on which Orozco “built” his famous engraving know as Mexican Pueblo.

Fig. 10. Drama (1930).
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes y Beatriz Eugenia Mackenzie.
Fig. 11. The Vigil (1929).
J.C. Orozco. Miriam Molina.

Fig. 12. Explosion (n.d.).
J.C. Orozco. Miriam Molina.
Fig. 13. Maguey (1932).
J.C. Orozco. Miriam Molina.

Fig. 14. Aquella noche (That night) (1930).
J.C. Orozco. Miriam Molina.
Fig. 15. Échate la otra (Have another) (1935). Colección INBA/MACG.

Fig. 16. Boceto para ballet I (Sketch for a ballet I) (1945) Colección INBA/MACG
Fig. 17. Guerra II (War II) (1926-1928)
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes and Beatriz Eugenia Mackenzie.

Fig. 18. Homecoming of the Worker of the New Day (1930-1931)
The New School for Social Research.
It is no coincidence that this white cube was built by Orozco in both his houses in the city of Guadalajara (814 López Cotilla St and 27 Aurelio Aceves St), which makes it clear that the famed muralist was resolved to bring to practice his ideas and vision about modern architecture, leaving no doubt about his participation in the project.

Fig. 19. “White cube” on the rooftop of the Home-and-Studio at López Cotilla St.
Photograph by Luis Francisco Copado Leos.
Fig. 20. “White cube” on the rooftop of the Aurelio Aceves St. Home-and-Workshop. Google Maps
Other than the white cube, another precise element that recurrently appears in Orozco’s engravings about architecture are the changes in the level or height on some walls appearing in his drawings. These “jumps” in the walls that the painter reproduces intentionally in the design of the López Cotilla St. Home-and-Studio bring out its presence and give strength to the building’s visual image.

Fig. 21. The Stoning of Saint Stephen. (1949)
Fine Art America.
Fig. 22. Mexican House (1929).
J.C. Orozco. Miriam Molina.

Fig. 23. Durmiendo (La familia) (Sleeping) (The Family) (1930).
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes and Beatriz Eugenia Mackenzie.
Fig. 24. Colinas mexicanas (Mexican Hills) (1930). Colección INBA/MACG.

Fig. 25. La Casa de piedra (The House of Stone) (1929).
José Clemente Orozco, Pintura y Verdad. Miguel Cervantes and Beatriz Eugenia Mackenzie.

Figs. 26, 27, 28 and 29. Changes in the height of walls of Casa Orozco. Own photographs.

Figs. 30 and 31. Changes in the height of walls of Casa Orozco. Own photographs.
The aesthetic language of the Home-and-Studio, both in its totality as in its precise elements, matches that used by Orozco in his exercises of abstraction of Mexican architecture. This abstraction is also distinguishable in the design of the Home-and-Studio, which, in a similar manner to the pictures, endeavors to reduce architecture to its most basic forms and to do without any decorative element, which doubtlessly reinforces the argument of his participation in the design.
It is not a coincidence that Orozco carried out most of the pictures (engravings) on abstraction of architecture during his stay in New York (1927-1934). It was in this city that the famed painter grew fond of the technique of engraving. It was also in this place where, thanks to Frederick Kiesler, he became knowledgeable on modern architecture 18. It was also there where he studied and put in practice the geometrical principles of dynamic symmetry, developed by the Canadian geometrician Jay Hambidge.19
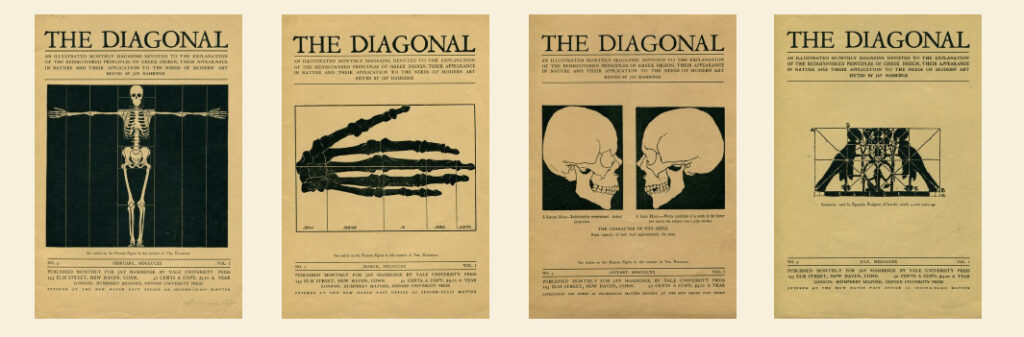
Fig. 32. Some covers of The Diagonal, magazine which spread the writings by Jay Hambidge on dynamic symmetry.
Blog Art IMHO http://mirtarotondo.com/blog/jay-hambidge/
Jay Hambidge had devoted himself to the study of geometry and the relationship between art and natural structures, including that of the human body and those defining the growth of plants. Hambidge described, parting form these studies, dynamic symmetry, which is, in his own words, the principles of design to be found in the architecture of man and plants20. The application of dynamic symmetry extended throughout North American art and design during the 1920s and 1930s21. Dynamic symmetry appears in rectangles, with a ratio of sides which is incommensurable, but commensurable when squared22. For example, a ratio of 1:√2 is incommensurable, being √2 an irrational number. However, if squares are built from the greater and lesser sides of the rectangle, these will have areas of 1 and 2 square units, respectively (as shown in fig. 33), resulting in a radio of 1:2 between the areas.

Fig. 33. Root-two rectangle. The radio 1: √2 is incommensurable, but commensurable when squared, fulfilling the main criterion of dynamic symmetry. Own elaboration.
Dynamic symmetry is based on the square, its diagonal and the diagonal of its half23. From these elements, an infinity of geometric shapes can be reproduced, which will, in turn, have the capacity to reproduce themselves. This is the distinction between dynamic and static symmetry, the latter lacking this trait of growth.

Fig. 34. Diagram of a square, its diagonals, its bisection and the diagonal of its bisection. Own elaboration.
From these elements, what Hambidge names root rectangles (fig. 35) can be reproduced. These are one of the main elements for the application of dynamic symmetry in art and design. In addition, these relate to the golden ratio, as shown in figure 36.
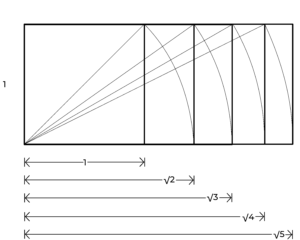
Fig. 35. Construction of root rectangles up to root-five. Own elaboration, from Hambidge.
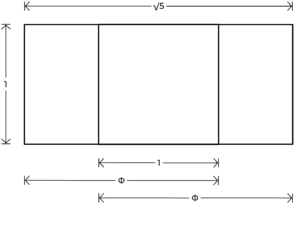
Fig. 36. Relationship between the golden rectangle and the root-five rectangle. Own elaboration, from Hambidge.
From the described quadrilaterals, it is possible to build rectangles of different ratios that maintain the trait of dynamism. Hambidge describes some of the most common ratios in nature and art that apply dynamic symmetry. Below, some of these, along with their reciprocal, their half and the reciprocal of their half, are reproduced. As can be observed, these are compound dynamic rectangles are composed, in turn, by other simple dynamic rectangles, mainly squares (S), golden rectangles (WS) and root-five rectangles (√5).
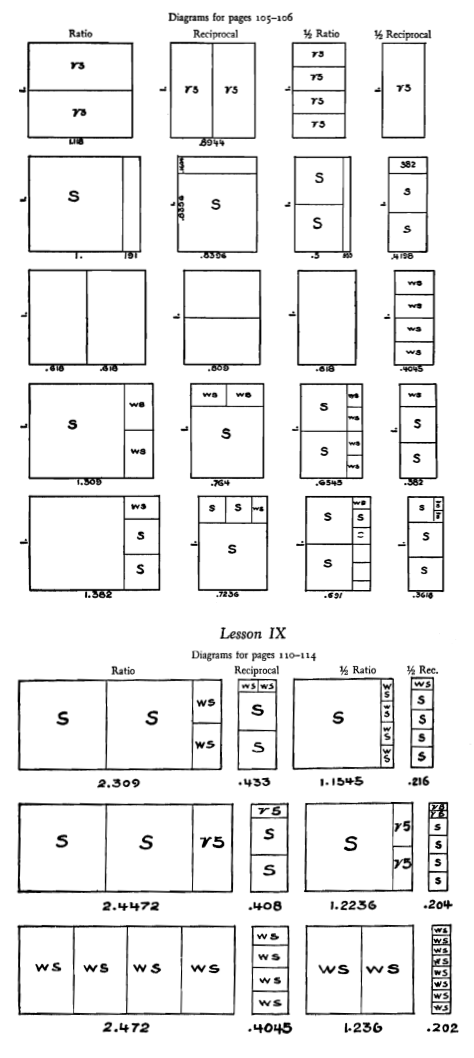
Fig. 37. Some of the ratios listed by Hambidge as the most commonly found in art and design that apply dynamic symmetry, as well as in nature. The Elements of Dynamic Symmetry. Jay Hambidge.
To further understand the subject at hand, the papers of the geometrician Rachel Fletcher on dynamic rectangles, included in the Bibliography section and available at the end of this text for their download.
Orozco experimented with the use of dynamic symmetry in his murals Result of this are the frescoes of his authorship in the building of the New School for Social Research in New York. Strong geometrical figures, diagonals and straight angles are distinguishable in the murals’ composition, product of the rigorous method used to obtain them.

Fig. 38. The struggle in the East (1931).
https://www.newschool.edu/university-art-collection/re-imagining-orozco-exhibition-essay/

Fig. 39. Table of Universal Brotherhood. (1931). Both murals were carried out in the New School for Social Research.
https://www.newschool.edu/university-art-collection/re-imagining-orozco-exhibition-essay/
In his Autobiography, Orozco dedicates a chapter to speak about dynamic symmetry and the murals at the New School for Social Research. In it, he reflects on the fact that the main service of dynamic symmetry to the arts was to provide geometry as a tool. He closes explaining the following:
After the painting at the New School, I abandoned the very rigorous and scientific methods of dynamic symmetry, but I kept what was fundamental and inevitable of what was learnt, in order to forge new work methods. I had the explanation of many previous mistakes, and I found new pathways.24
This way, some of these ideas on geometry persist, in a more subtle way, in his muralistic cycle of Guadalajara and his later works. Orozco rescued many of the fundaments of geometry from his use of dynamic symmetry. References and aesthetic canons can be found in his later work. The dome of the University Hall (fig. 40) contains the diagrams corresponding to the square, its bisection and its diagonals, and the construction of the golden rectangle and the root-two rectangle.

Fig. 40. Detail of the dome of the University Hall. Note the diagrams of geometrical plans at the center of the image.
Tráfico ZMG. https://traficozmg.com/2017/05/concluye-restauracion-murales-orozco-paraninfo-la-udg/

Fig. 41. Composition of one of the murals at the University Hall from the golden spiral.
Own elaboration on photograph from José Clemente Orozco, Pintura y Verdad. Miguel Cervantes and Beatriz Eugenia Mackenzie.
From the graphic work created by Orozco during his stay in New York, the picture called Mexican Pueblo stands out for its importance and its relationship to the design of the Home-and-Studio. He produced this work in 1930, practically at the same time he painted the murals at the New School for Social Research. During this stage, the muralist experimented with the reach of Hambidge’s Dynamic Symmetry.

Fig. 42. José Clemente Orozco. Mexican Pueblo (1930) MoMA Collection, New York.
https://www.moma.org/collection/works/77130
This engraving shows like no other Orozco’s vision of modern architecture. The rigid application of dynamic symmetry is used to create a rich and complex composition, in which the use of diagonals stands out, along with the appearance of the white cube at the center of the picture, and, to its right, the change in height, or jumps in a wall. If the picture is observed meticulously and compared to the aesthetic language used in the project of the Home-and-Studio, the same coincidences can be clearly distinguished in both projects.
This work had a great influence on Luis Barragán. Proof of this is the fact that an enlargement of it hangs on one of the walls of his home and studio in Mexico City, and of which the prestigious architect expressed the following:
I want you to observe this lithography by Orozco. He painted the shadows where the light goes, and light where the shadows go, this is something that goes beyond what we see, it is something magical. This is why the painter describes it to us, because he can go beyond the physical limitations and teach us what we cannot see. There is a great lesson of architecture that we must learn from this.25

Fig. 43. Cuadro Mexican Pueblo en la estancia de la Casa Luis Barragán. Fotografía de Alberto Moreno Guzmán.
https://unavidamoderna.tumblr.com/post/116144958548/estancia-de-casa-barrag%C3%A1n-calle-general-f
Mexican Pueblo is a lithography dating from 1930. The original plate is of José Clemente Orozco’s authorship. From it, one hundred prints were made. The printing was in charge of George C. Miller, and its distribution, of Delphic Studios, both based in New York. The composition measures 38.8 x 27.7 cm (15 1/4 x 10 7/8”), on a 56.2 x 40.5 cm (22 1/8 x 15 15/16”) sheet26. It has the print number on its bottom left corner, and the author’s signature, on the bottom right corner.
Mexican Pueblo es una litografía fechada en 1930. La placa original es de autoría de José Clemente Orozco. A partir de ella, se realizaron cien impresiones. La impresión estuvo a cargo de George C. Miller, y su distribución, de Delphic Studios, ambos con sede en Nueva York. La composición mide 38.8 x 27.7 cm (15 1/4 x 10 7/8”) sobre una hoja de 56.2 x 40.5 cm (22 1/8 x 15 15/16”)26. Cuenta con el folio en la esquina inferior izquierda, y la firma del autor, en la esquina inferior derecha.
Five cubical volumes predominate the composition. Two of them have doors. They all lack windows. The volume of the top left corner has a turret on its higher end, while the one on the extreme right has two changes, or jumps of height. The rest of the volumes maintain regularity on their edges.
Two of these volumes project shadows to their left side, while the remaining three project them to their right. Both the illuminated faces of the volumes as the projected shadows are disposed in way that all the superior edges form diagonal lines. Three of them are parallel to each other: the top edge of the central volume, and the two of lower height of the volume at the extreme right. The shadows projected by the volumes vary in intensity, from a mid-tone gray to a completely black plane.
In addition to the described volumes, four rocky solids and a dark platform in the bottom right corner, that could, or not, be a part of the former, can be found. The sky that makes up the composition’s background holds a relatively uniform tonality.
Fifteen women, completely covered, save their faces, occupy the scene, situating themselves on the largest rocky solid. The women group together behind a male character of short height, who holds an object in his right hand. He may be, perhaps, a child or a guide.

Fig. 44. José Clemente Orozco. Mexican Pueblo (1930). MoMA Collection, New York.
https://www.moma.org/collection/works/77130
– With the purpose of identifying and analyzing them, the cubical volumes were numbered from 1 to 5, and the rocky solids, from “a” to “d”.
– Most of the vertical edges of the cubical volumes, as well as of the dark platform of the bottom right corner (cyan) are parallel to the vertical margins of the composition. The exception to this are those that make up the turret and the jumps in the volume of the extreme right, which have a slight tilt.
– The top border of the dark platform in the bottom right corner, as well as of the rocky solid “b” (green) are parallel to the horizontal margins of the composition.

Fig. 44.1 Geometric construction from figure 44.
The composition of the engraving Mexican Pueblo is inscribed on a rectangle, whose sides hold the ratio 1:√2, as illustrated in figure 45. Following the method described by Hambidge to construct a root-two rectangle27:
– Draw an AEJP square from the composition’s height, which is to way, line AE (27.7 cm), equivalent to one unit.
– Obtain the length of the diagonal AJ of this square from the Pythagorean Theorem, which indicates that the square of the hypotenuse (AJ) is equal to the sum of the squares of the legs (AE and EJ). Which is to say, in units, 12+12=22. In centimeters, 27.72+27.72≈39.172. The diagonal (AJ) of the square has a length of 39.17 cm.
– With the compass point set on point A and an AJ radius, draw a curve to point O, and extend the line AO. In other words, AO has the same length as AJ, of 39.17 cm, or √2 units.
– From points E and O, draw lines EK and KO, closing the rectangle (AEKO).
– The AEKO rectangle, obtained from this process, holds a 1:√2 ratio, with a height of 27.7 centimeters and a length of 39.1 centimeters. When these measures are compared to those in the MoMA’s artwork label (38.8x27.7cm), they practically match those of the AEKO rectangle (39.17x27.7cm). The difference may be caused by the fact that only two decimal places were used to carry out the operation.

Fig. 45. Construction of a root-two rectangle over Mexican Pueblo (1930). Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– The bottom right edge of the d rocky solid (blue) is parallel to AJ diagonal. In addition, the shadow of volume 5 seems to relate to curve JO.

Fig. 45.1. Geometric construction from figures 44 and 45.
The diagonal is the base of dynamic symmetry. Hambidge mentions that For purposes of design the most important element of a rectangle is its diagonal28. Most of the lines and verifications in dynamic symmetry are traced based on diagonals. A rectangle’s diagonals are those that cross the rectangle from a corner to the opposite corner. Each rectangle has two, one in each direction.
– From the corners of rectangle AEKO, its diagonals are drawn (red).
– The diagonals AK and EO intersect at point I’.
– From point I’, line HR is drawn, in suck way that it is parallel to the height of rectangle AEKO.
– The HR line divides the AEKO in two halves (transversal bisection), forming two rectangles: AEHR and RHKO.
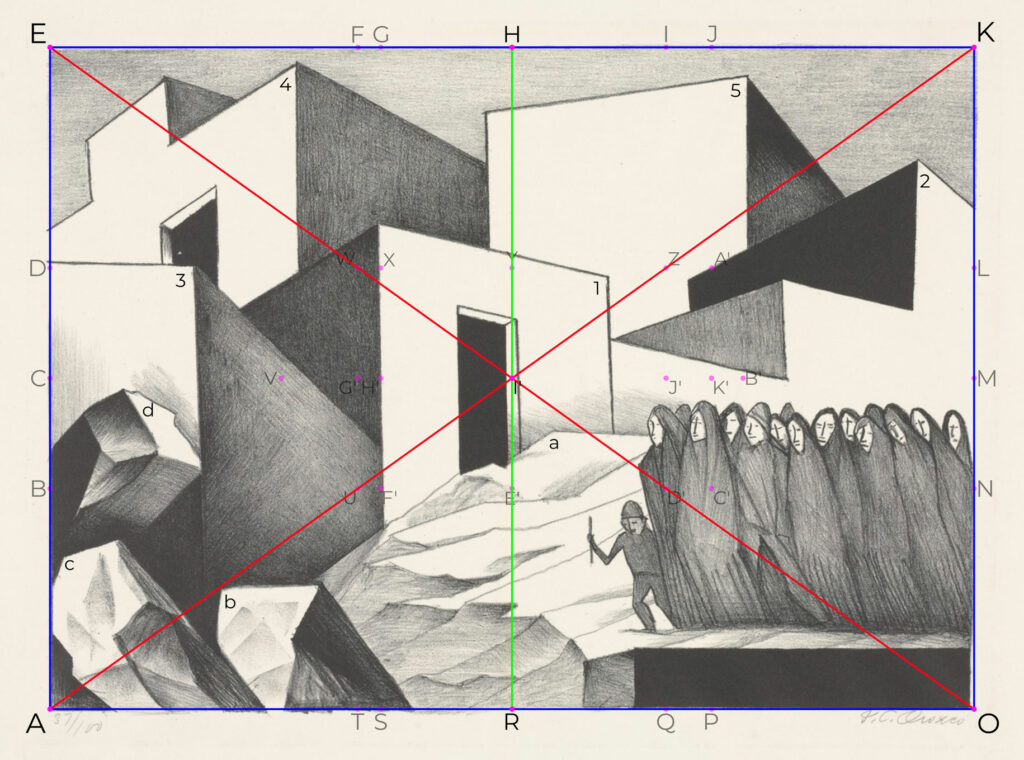
Fig. 46. Transversal bisection of the rectangle containing the lithography Mexican Pueblo (1930) drawn from its diagonals. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
Root rectangles have the peculiarity of being able to be subdivided into rectangles with the same ratio (in this case, 1:√2) from their diagonals. This faculty of “movement” is what Jay Hambidge calls dynamism.29
Rectangles AEHR and RHKO are reciprocal to rectangle AEKO. This means that, while rectangle AEKO holds a 1:√2 ratio between its sides, in such way that it has a horizontal orientation, AEHR and RHKO are similar, but with a √2:1 ratio, which is to say, they have a vertical orientation. To verify the above statement, and with a similar process to that applied in figure 45:
– Draw a square from the lesser side of the rectangle (AR for rectangle AEHR).
– Using a compass, draw a line (dotted) from the diagonal of the square to the point where it intersects with the opposite side of the rectangle (HR). Verify that this intersection is on point H.
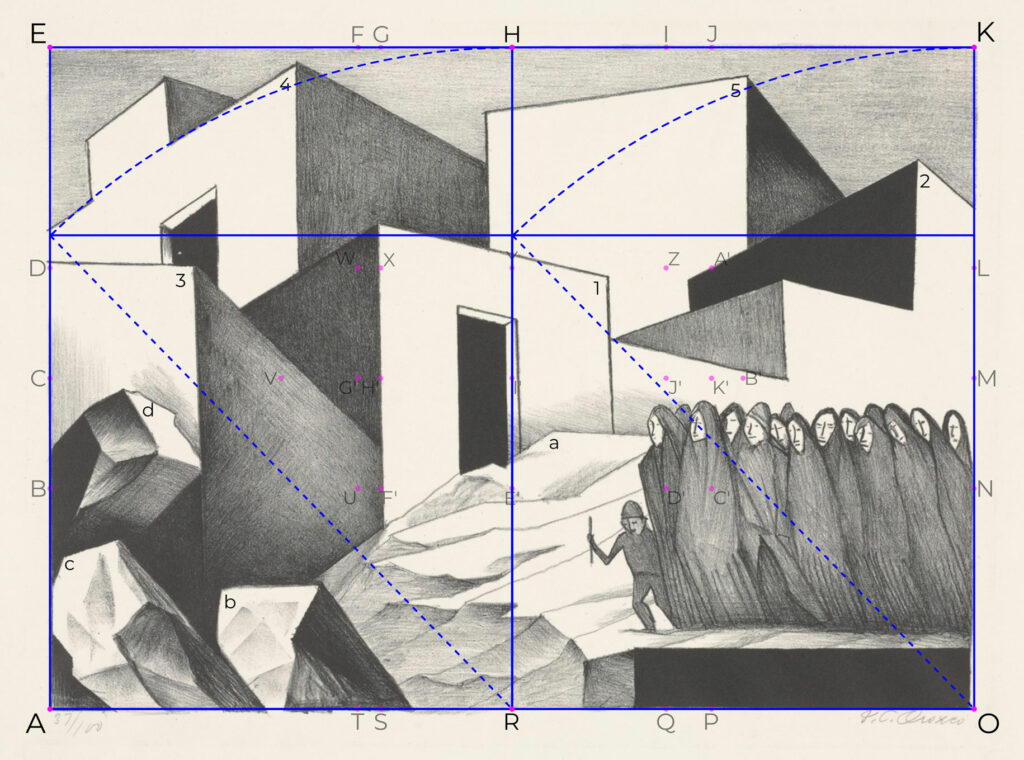
Fig. 46.1. Verification of dynamism of root-two rectangle on the lithography Mexican Pueblo (1930) from its transversal bisection. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– The top borders of volume 4 and its turret (magenta) are practically parallel to diagonal AK.

Fig. 46.2 Geometric construction from figures 44, 45, 46 and 46.1.
In addition to its diagonals (AK and EO), each rectangle has four reciprocal diagonals (AH, HO, ER and RK), corresponding two to each “greater” diagonal. Each reciprocal diagonal starts at a corner of the rectangle (points A, E, K and O) and is perpendicular to a “greater” diagonal (AK or EO). Just as the greater diagonals, reciprocal diagonals play a fundamental part in dynamic symmetry.
In the case of root-two rectangles, an end of reciprocal diagonal matches an end of the rectangle’s bisection. With this established, it is possible to obtain the reciprocal diagonals of rectangle AEKO:
– Draw a line from the corner (A) to the furthest end of the rectangle’s bisection (H=, thus obtaining the reciprocal diagonal AH.
– Repeat the process on the three remaining corners, thus obtaining lines ER, RK and HO.
– The reciprocal diagonals AH and RK are parallel to each other and perpendicular to the greater diagonal EO. The reciprocal diagonals ER and HO are parallel to each other and perpendicular to the greater diagonal AK.
– Reciprocal diagonals correspond, in turn, to the greater diagonals of the reciprocal rectangles. In this sense, ER and AH are the greater diagonals of the reciprocal rectangle AEHR; and RK and HO are the greater diagonals of reciprocal rectangle RHKO.
– From the intersections between reciprocal diagonals (V and B’), draw a horizontal line (CM), and extend it until it meets rectangle AEK at C and M points. CM line divides the AEKO rectangle in two equal parts (longitudinal bisection).

Fig. 47. Greater and reciprocal diagonals of the rectangle containing the lithography Mexican Pueblo (1930) and the bisections of the rectangle obtained from these. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– CM and HR bisections, drawn from the mentioned diagonals, divide the AEKO rectangle in four equal parts: ACI’R, CEHI’, I’HKM and RI’MO, all of them root-two rectangles.
– This can be verified with the same method used it figures 45 and 46.1, as shown in figure 47.1
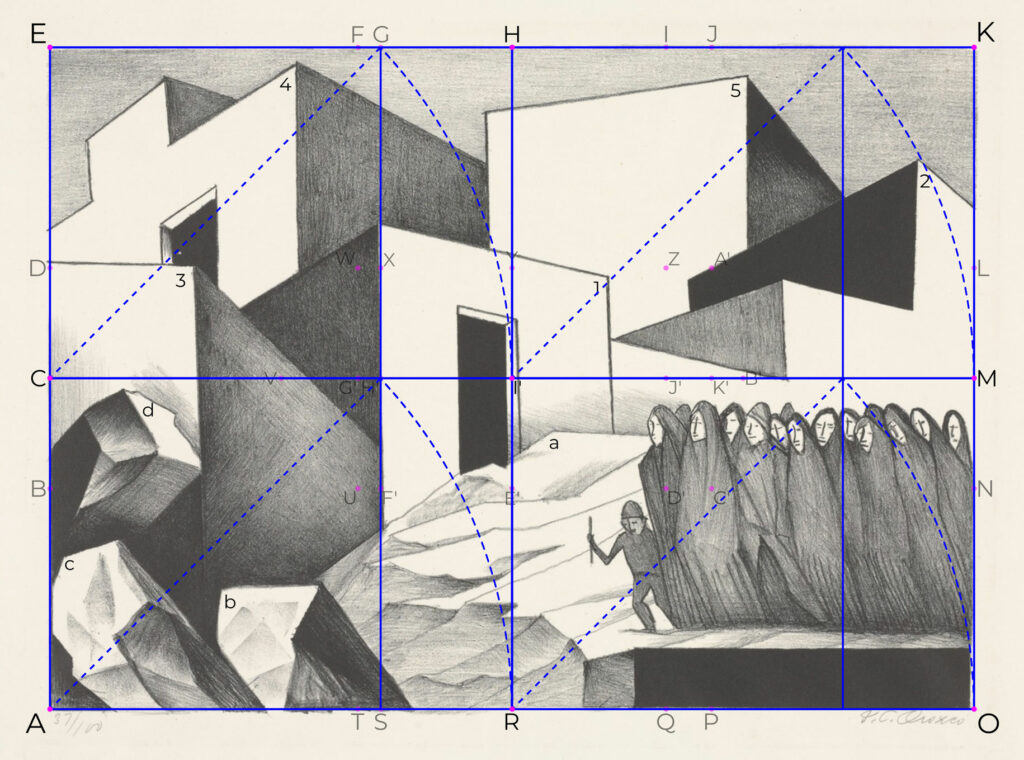
Fig. 47.1 Verification of dynamism of the root-two rectangle containing the lithography Mexican Pueblo (1930). Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
https://www.moma.org/collection/works/77130.
– Alternatively, the similarity between rectangles ACI’R, CEHI’, I’HKM, RI’MO and AEKO can be verified by observing that their greater diagonals, in one direction or the other, are parallel (in other works, AK is parallel to CH, AI’, I’K and RM, shown in red, and EO is parallel to CR, EI’, I’O and HM, in green).

Fig. 47.2 Alternative verification of dynamism of the root-two rectangle in which the litography Mexican Pueblo (1930) is contained, using its diagonals. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– None of the diagonals of the volumes or their shadows match or are parallel to the greater diagonals of the rectangle or to its reciprocal diagonals. However, the shaded side of rocky body b forms a line (yellow) that is parallel to the ER reciprocal diagonal.

Fig. 47.3 Geometric construction from figures 44, 45, 46, 46.1, 47, 47.1 and 47.2
From the intersections of the reciprocal diagonals with their corresponding greater diagonal, the root-two rectangle can be divided, and its dynamism verified, with the following process:
– Draw a line (FT) from intersection U to intersection W, and it is extended until it intersects with the AEKO rectangle (at points F and T).
– Draw a line (DL) from intersection W to intersection Z, and it is extended until it intersects with the AEKO rectangle (at points D and L).
– Draw a line (IQ) from intersection Z to intersection D’, and it is extended until it intersects with the AEKO rectangle (at points I and Q).
– Draw a line (BN) from intersection D’ to intersection U, and it is extended until it intersects with the AEKO rectangle (at points B and N).

Fig. 48. Subdivision of the rectangle containing the lithography Mexican Pueblo (1930), using the intersections of its greater and reciprocal diagonals. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– Applying the same process used in figures 45, 46.1 and 47.1, consisting of drawing a square and compass line, it can be verifies that the nine resulting rectangles are root-two rectangles.

Fig. 48.1 Verification of the dynamism of the root-two rectangle containing the lithography Mexican Pueblo (1930). Own elaboration from image from the MoMA of New York Collection.
https://www.moma.org/collection/works/77130.
– Alternatively, the similarity between the ABUT, BDWU, etc. and the AEKO rectangles can be verified with the observation their greater diagonals, in one direction and another, are parallel (in other words, AK is parallel to DF, BW, WI, etc., in red; and EO is parallel to BT, DU, UQ, etc., in green).

Fig. 48.2 Alternative verification of dynamism of the root-two rectangle containing the lithography Mexican Pueblo (1930) using its diagonals. Own elaboration from image from the MoMA of New York Collection.
https://www.moma.org/collection/works/77130.
– Since the generated segments in previous figures are all parallel to those previously analyzed, no new relationships to the lines of the lithography Mexican Pueblo were found. Mexican Pueblo.

Fig. 48.3 Geometric construction from figures 44, 45, 46, 46.1, 47, 47.1, 47.2, 48, 48.1 and 48.2.
Hambidge explains that dynamic symmetry is based on the square, its diagonals, its bisection, and the diagonals of its bisection30. As it was proven in figure 45, a root-two rectangle is constructed from a square and its diagonal. With the objective of analyzing the rest of the elements of such square:
– Draw an AEJP square (magenta) from the AE line.
– Draw its AJ and EP diagonals (green), joining the opposite corners of the AEJP square.
– Draw a GS vertical line (cyan) from the intersection of the AJ and EP diagonals.
– Extend lines from the corners to points G and S, thus obtaining the diagonals of the square’s bisection (AG, GP, ES and SJ, yellow).

Fig. 49 Square used to construct the root-two rectangle containing the lithography Mexican Pueblo (1930), its diagonals, bisection, and diagonals of its bisection. Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– The shadow projected by volume 3 (yellow) forms a line parallel to the diagonal of the square (EP).
– The bisection of the square (GS) aligns almost perfectly with the vertical edge that divides the lit and the dark faces of volume 1. This is highly significant, since this “white cube”, previously mentioned as a recurring element in Orozco’s oeuvre, is the central element of the composition.

Fig. 49.1 Geometric construction from figures 44, 45, 46, 46.1, 47, 47.1, 47.2, 48, 48.1, 48.2 and 49.
From the previously developed processes, a grid, illustrated in figure 50, was constructed in order to analyze the geometrical construction of the composition. For this effect:
– The AEJP square (magenta) and the AEKO rectangle (red) generated from it are integrated from figure 45.
– The HR transversal (cyan) and CM longitudinal bisections of rectangle AEKO, generated in figures 46 and 47, are integrated.
– The grid generated in figure 48, representing the subdivision of the AEKO rectangle in nine similar rectangles, is integrated. This includes BN, DL, FT and IQ lines (blue).
– The bisection of AEJP square (green) is integrated, as drawn in figure 49.

Fig. 50. Grid used fot the analysis of the geometry of the lithography Mexican Pueblo (1930). Own elaboration from image from the MoMA of New York Collection. https://www.moma.org/collection/works/77130.
– The shadow of volume 1 (dark green) is parallel to H’K.
– The top shadow of volume 2 (brown) is parallel to AK’.
– The bottom shadow of volume 2 (violet) is parallel to CK.
– The shadow of volume 4 (dark red) is parallel to GM.
– The shadow of volume 4's turret (black) is parallel to EM.
– The shadow of volume 5 (orange) and the rightmost diagonal of rocky body c (orange) are parallel to JM.
– The top border of volume 1 (light pink) and the mid and bottom borders of volume 2 (light pink) are parallel to EL.
– The top border of volume 2 (dark blue) is parallel to JL.
– The top border of volume 5 (gray) is parallel to CL.
– The top border of volume 2 (pink) is parallel to JQ, and its bottom border (light blue), to IP.
– The vertical borders of volume 4's turret (gold) are parallel to FX.

Fig. 50.1 Geometric construction from figures 44, 45, 46, 46.1, 47, 47.1, 47.2, 48, 48.1, 48.2, 49 and 50.
As it was mentioned above, Orozco dedicated part of his stay in the United States, after the moment he met Mary Hambidge, to study and apply dynamic symmetry in his works. It is difficult to analyze Orozco’s work during this period if only Hambidge’s publications on the topic are taken into account, leaving aside the advances and interpretations that the Zapotlense artist could have made on the work of the geometrician.
In order to broaden the vision and application of Orozco regarding the use of the diagonal and dynamic symmetry, his Notebooks (Cuadernos), organized and published by Raquel Tibol are of great value. The Notebooks date from between 1931 and 1934, which is to say, Orozco produced them, mostly, during his stay in the United States, and completed them during the first months of his return to Mexico31.
In his notes, Orozco refers in his notes to the different diagonals of a rectangle. He mentions, as fundamental diagonals: he agrees with what Jay Hambidge mentioned, referring to the general (or greater) diagonals, reciprocals, of the halves, and ands the diagonals of the quarters (fig. 51)32. In another annotation, he draws a diagram about the use of reciprocals in the construction of a composition (fig. 52). In it, the greater diagonals and the longitudinal and transversal bisections of the rectangle divide it into four similar parts, each crossed by a greater diagonal. Orozco drew the reciprocal diagonals of each partially, forming a polygon with a shaded interior.33

Fig. 51. Fundamental diagonals.
Fig. 52. Reciprocals as an element for construction.
Cuadernos, José Clemente Orozco.
Throughout his Notebooks, Orozco refers in several occasions to the use of “systems”. He schematically lists the use of greater, reciprocal and diagonals of the halves, agreeing with what Hambidge had explained, under the title Different systems of diagonals (fig. 53). 34

Fig. 53. Different systems of diagonals. Cuadernos, José Clemente Orozco.
Another annotation, about Juxtaposed areas and superposed areas, followed by another under the title Diagonal of each area35, stands out. Some diagrams, seemingly Orozco’s original work based on Hambidge’s texts, explain the use of “areas” in a composition, and to the use of diagonals in every one of these areas (fig. 54), going beyond the diagonals of the greater or general rectangle (or the rectangle containing the totality of the composition). It is worth noting that in these notes, Orozco admits both the juxtaposition and the superposition of areas.
The possibility of superposing and juxtaposing areas in a composition and of exploring the use of diagonals of each area takes Orozco to create images that differ from what he would have achieved if he had limited exclusively to applying the methods of dynamic symmetry in a strict manner. In addition, observing this along with the annotation on different systems (fig. 53) opens the possibility to use different diagonal system in each area of the composition.
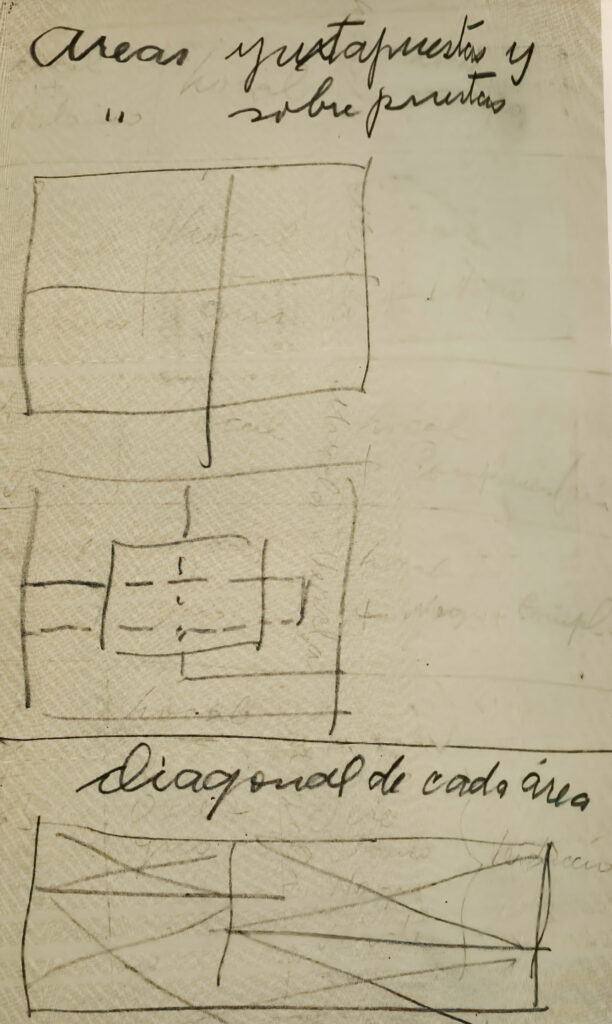
Fig. 54. Superposition and juxtaposition of areas. Cuadernos, José Clemente Orozco.
Finally, a note where Orozco refers to the diagonals of the golden section (fig. 55)36 also stands out. In it, he sectioned the rectangle in length and width by dividing their sides by the golden ratio. This division results in four areas. He drew the transversal and longitudinal bisections of each one, as well as their greater diagonals.

Fig. 55. Diagonals of the Golden ratio. Cuadernos, José Clemente Orozco.
Based on Orozco’s Notebooks and Jay Hambidge’s Elements of Dynamic Symmetry and Dynamic Symmetry in Composition as used by the Artists, Casa Orozco’s façade was analyzed as follows.
The façade of the Home-and-Studio is synthetized into a cubical volume, completely pure and clean, only broken by the access door and the two windows. The elements that make up the exterior bring together an asymmetric, but visually balanced, composition. The façade, like the rest of the Home, contains only straight angles. The only diagonals or inclinations found are the details on the gate’s metalwork.
The windows have the same width, and they align vertically. The top one is the “window to the skies”, which breaks the austral wall of the higher rooftop. The bottom one, with twice the height of the “window to the skies”, opens to the studio.
The stairs close the difference of height between the sidewalk and the interior of the building. The low walls that limit the front gardens have three jumps, or changes, of height: one, on the eastern low wall, besides the access door; another, on the low wall that separates the western garden from the stairs; and the third, on the front low wall, divided by the gate.
The façade occupies the totality of the front of the property, with a width of 10.119 meters. The height is of 9.055 meters (see fig. 56). The ratio of these lengths is, approximately, of 1:1.118.
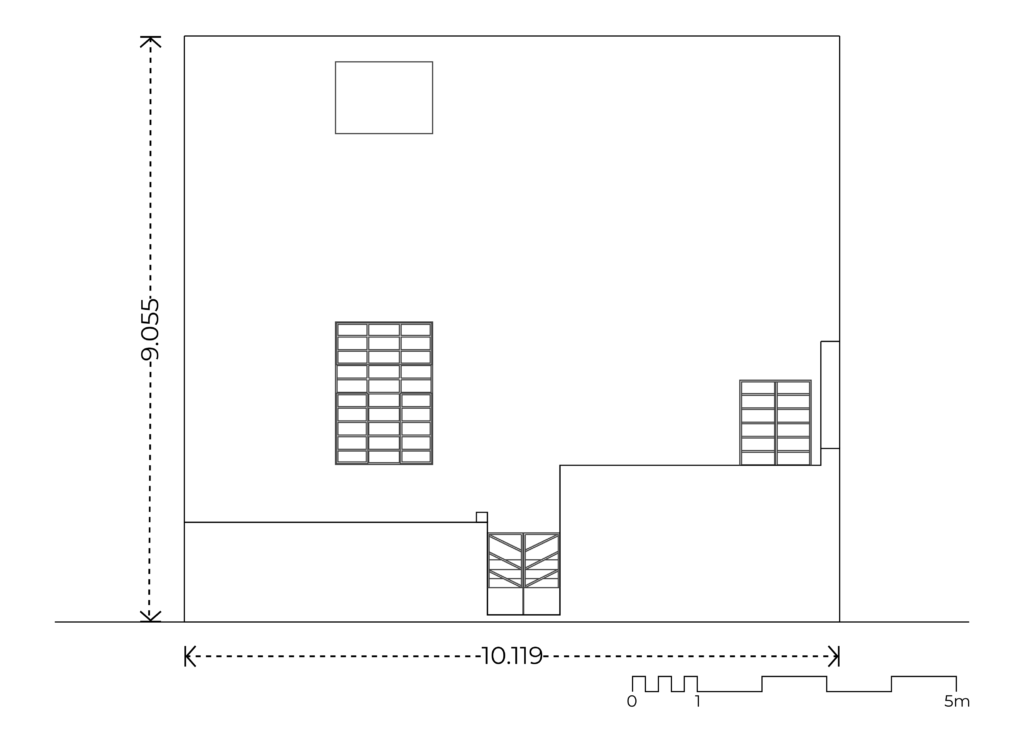
Fig. 56. Façade of Casa Orozco, its height and width. Own elaboration.
Jay Hambidge listed this ratio amongst those proportions found most frequently in Greek design and in nature37. Figure 56.1 shows some of the dynamic ratios that generate from the root-five rectangle, including 1:1.118.
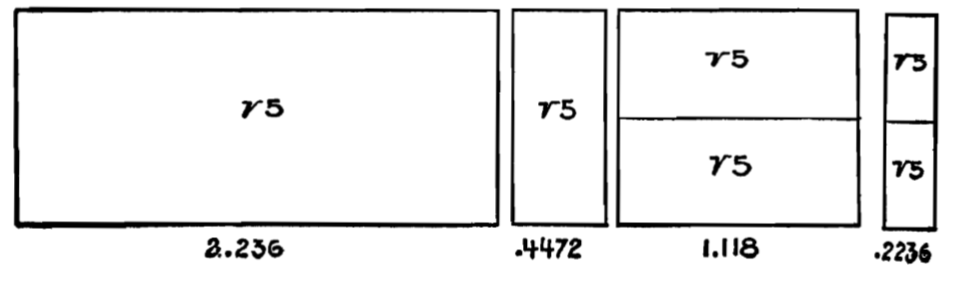
Fig. 56.1. Diagrams representing dynamic ratios: 1:2.236 (root-five rectangle), 1:0.4472 (its reciprocal rectangle), 1:1:118 (its half) and 1:0.2236 (half its reciprocal).
Elements of Dynamic Symmetry, Jay Hambidge.
It is possible to obtain the ratios shown above with the following procedure, as shown in figure 56.2.
– Draw an ABFG root-five-rectangle, with a height of 1 unit, its BG diagonal and its reciprocal diagonal AD.
– Draw line EH, dividing ABFG rectangle in halves.
– From the intersection of the reciprocal diagonal AD with rectangle ABFG at point D, draw line DI, closing the ABDI reciprocal rectangle.
– Draw line CJ, dividing the ABDI reciprocal rectangle in half.
– Verify that the resulting rectangles hold the dynamic ratios listed by Hambidge.
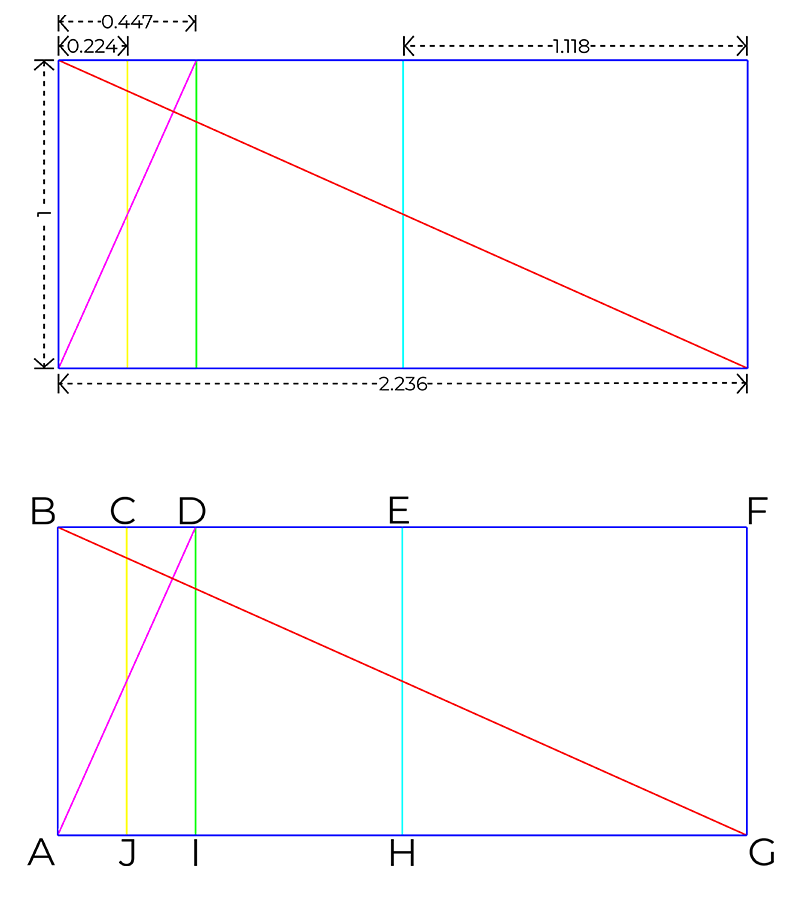
Fig. 56.2. Diagram of some dynamic ratios drawn from a root-five rectangle. Own elaboration based on Elements of Dynamic Symmetry, Jay Hambidge.
The façade of Casa Orozco matches the ratio of half a root-five rectangle, being its width 1.118 times its height. Alternatively, the 1:1.118 ratio can be described as two root five rectangles, stacked vertically.
To prove the ratio, two root-five rectangles are constructed from half the façade’s height, as show in figure 57. By superimposing the rectangles’ construction on the façade, it becomes evident that the resulting lines seem relate to the vertical borders of both windows, as well as the top border of the window to the studio.
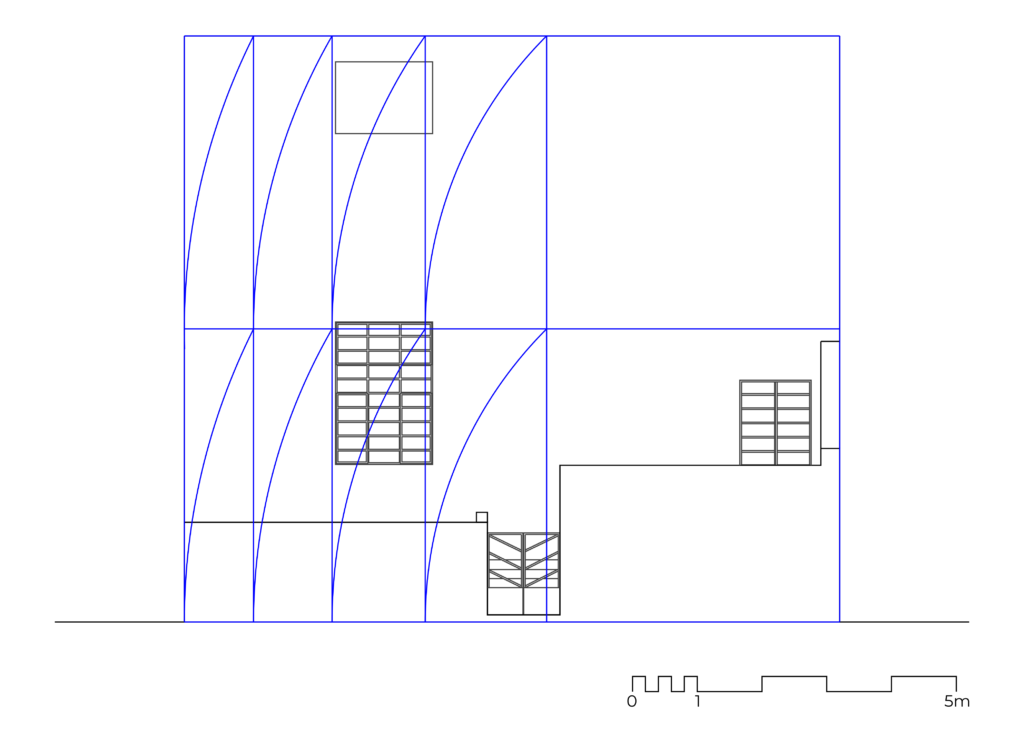
Fig. 57. Construction of root rectangles on the façade of Casa Orozco, based on Hambidge. Own elaboration.
Hambidge explains the process to “apply” the area of a square to the side of a rectangle38. “Applying” an area refers to obtaining a quadrilateral with the same area of that which originates it, but with a different ratio. The resulting lines divide the rectangle in four areas, two of them, similar to the rectangle.
This will result in a rectangle equal in area to the applied square. In order to obtain it:
– Draw an ACDH square from line AC (the shorter side of ACEG rectangle).
– Draw the AE diagonal.
– From point I, the intersection of the AE diagonal with DH line of the square, extend line BF, closing the ABFG rectangle. This is the “application” of the ACDH square: it has the same area, but a different ratio.
– The resulting ABIH and IDEF rectangles are similar to the ACEG rectangle.
– Line BF concurs with the longitudinal bisection of the “window to the sky”, or, in other words, it divides it in half, cutting through its shorter side.
– DH line nears the longitudinal bisection of the access door.
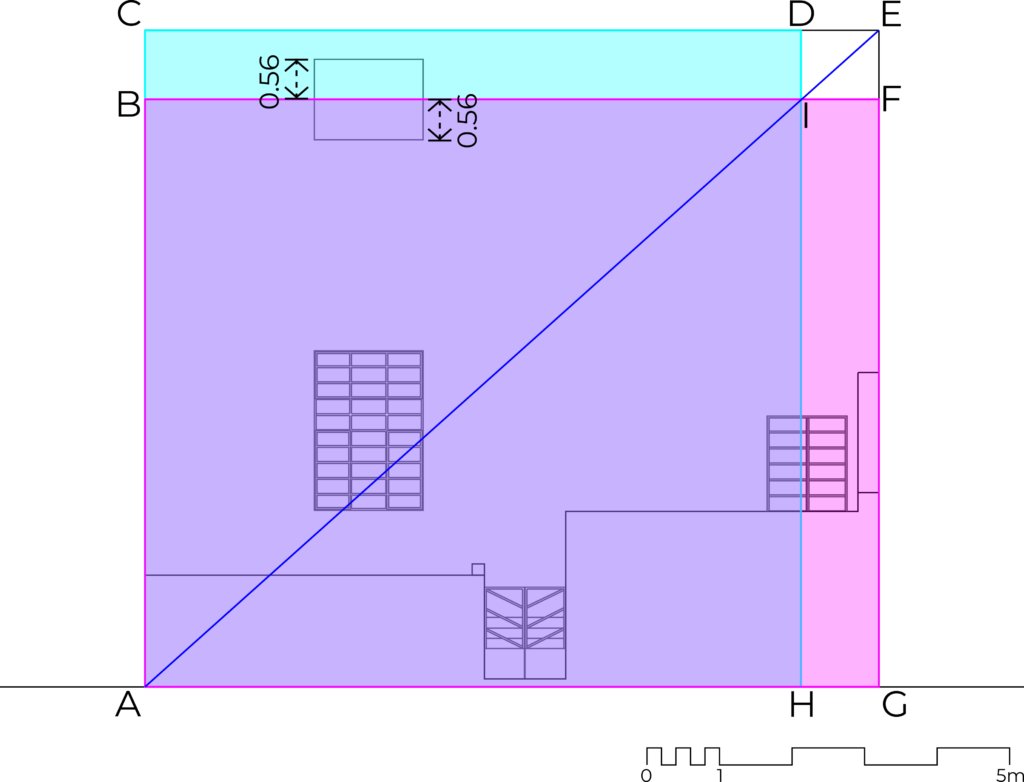
Fig. 58. “Application” of the area of a square to the façade of Casa Orozco. Orozco. Own elaboration.
– Draw an AFGL root-five rectangle from the height of the facade (AF), in such a way that AF is the longer side of the rectangle.
– Draw the diagonals (AG and FL) and its reciprocal diagonals (AJ, CL, DG and FI) of the AFGL root-five rectangle.
– Draw the BK and EH horizontal lines from the intersections of the diagonals and the reciprocal diagonals (N and M; and O and P, respectively).
– Line EH matches the bottom border of the “window to the sky” and BK line practically matches the top border of the front low wall.
– The resulting BEHK rectangle is, approximately, similar the studio window, both holding a ratio of 1:0.670. The half of the BEHK rectangle is, approximately, similar to the “window to the sky”, both holding a ratio of 1:1.342.
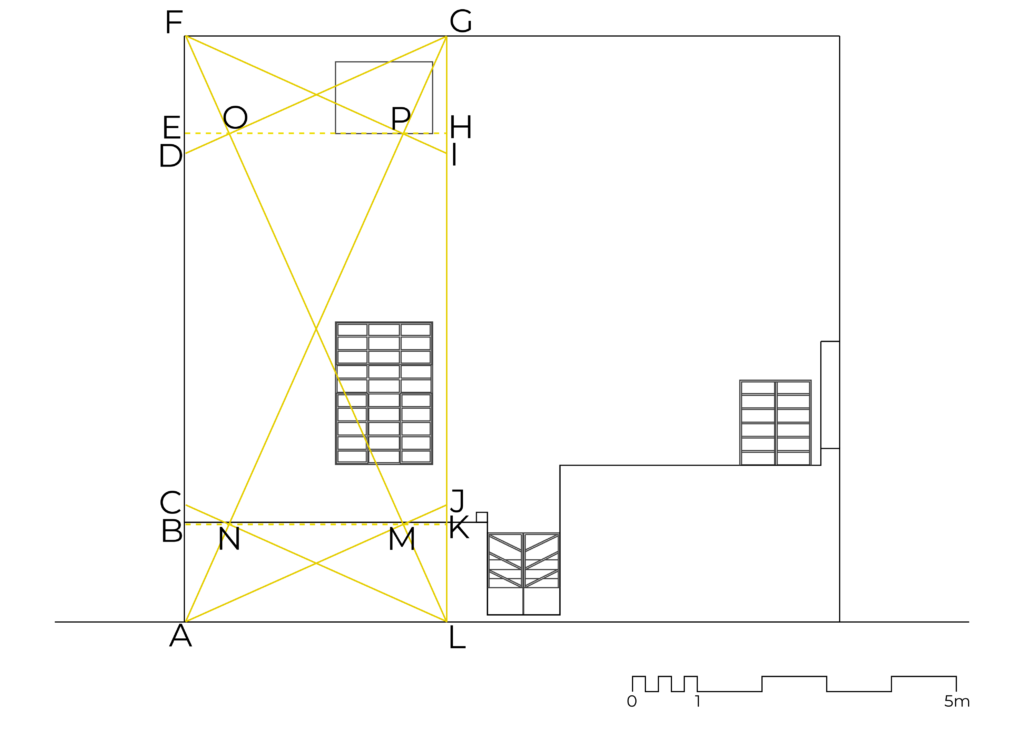
Fig. 59. Diagonals and reciprocal diagonals of a root-five rectangle applied to the façade of Casa Orozco. Own elaboration.
Based on the annotations in the Notebooks referring to areas and their diagonals (figs. 51-55):
– Extend the AM line from the top border of the eastern front low wall and the bottom border of the window to the studio.
– Extend the EH line from the eastern border of both windows.
– Extend the IJ line from the western border of the gate.
– Four areas result from this division. Two of the answer to dynamic ratios: the ADEH rectangle, with a radio of 1.73:1, matching a root-three rectangle oriented vertically; and the IJMN rectangle, with a radio of 1:2.236, matching a root-five rectangle.
– Draw the diagonals (AE and DH, red) and the reciprocal diagonals (AG, BH, CE and DF, green).
– Extend CF and BG lines (dotted orange) in order to close the ABGH and CDEF reciprocal rectangles.
– Line BG matches the top border of the window to the studio.
– In a similar process, draw the diagonals (IM and JN, red) and its reciprocal diagonals (IK, JP, LM and MO, green).
– Extend KP and LO lines to close the reciprocal rectangles IJKP and LMNO.
– The eastern border of the gate matches KP line.
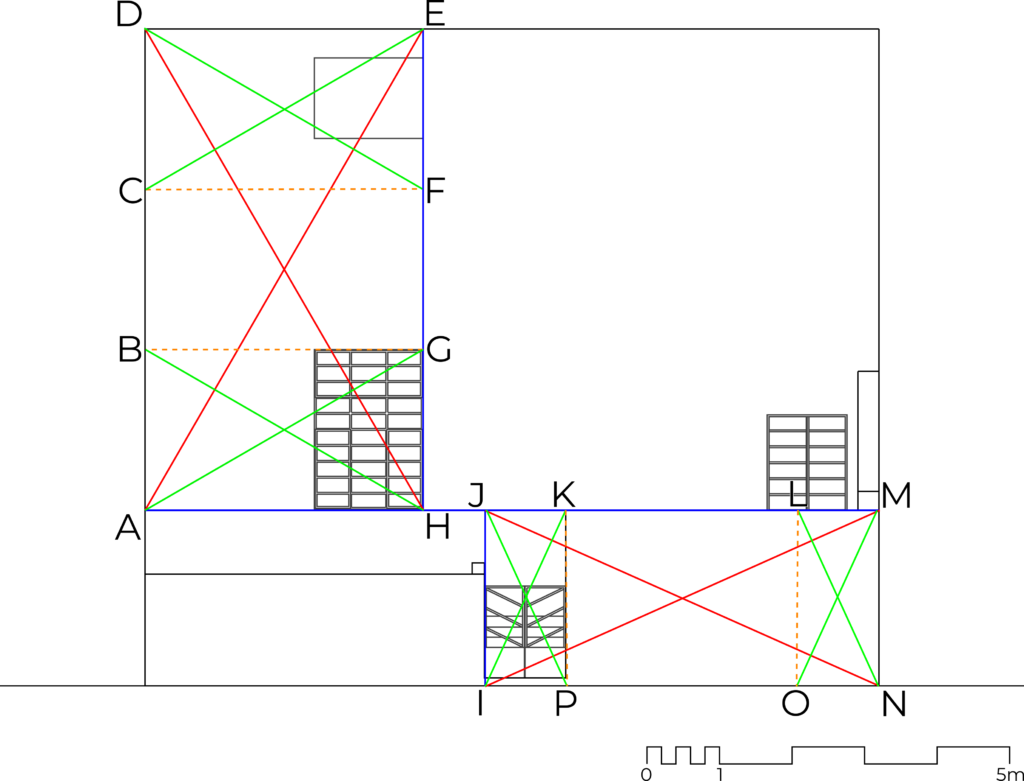
Fig. 60. Root rectangles in the composition of the façade of Casa Orozco. Own elaboration.
– The eastern low wall has a change in height. From the sidewalk level, the heights are 2.68 and 4.33 meters.
– The ratio between these heights is of 1:1.6180, in other words, the golden ratio, as shown in figure 61.
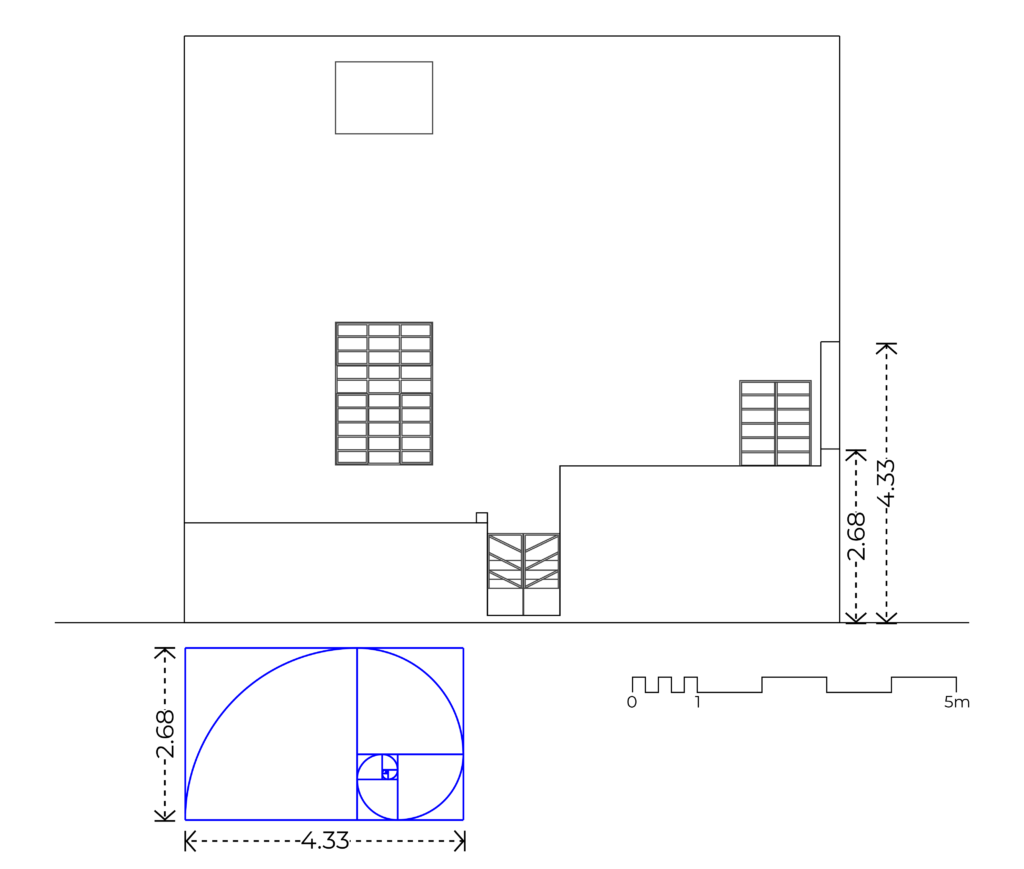
Fig. 61. Jump in heights of the eastern low wall of the façade of Casa Orozco. Own elaboration.
The presence of the principles of dynamic symmetry in the composition of the façade of Casa Orozco is very suggestive regarding the possible author, since it evidences the fact that the author must have had advanced knowledge of geometry and the application of Jay Hambidge’s ideas. This point doubtlessly counts in Orozco’s favor, since, as noted earlier, both his formation as his recent influences granted him this knowledge.
1. Valladares De Orozco, Margarita, and José Clemente Orozco. Cartas a Margarita: (1921/1949). Memorias / Testimonios. 1st ed. México: Ediciones Era, 1987. 294 [own translation]
2. Reed, Alma M. Orozco. Translation by Jesús Amaya Topete. 2a ed. México, D.F.: Fondo De Cultura Económica, 1983. 32 [own translation]
3. Orozco Valladares, Clemente. Orozco, Verdad Cronológica. Edited by Humberto Ponce Adame and Luz Rosalía Acosta, Martínez. Guadalajara, Jalisco: EDUG/Universidad De Guadalajara, 1983. 360 [own translation]
4. Orozco, José Clemente. Textos De Orozco. Mexico: Universidad Nacional Autónoma De México, 1983. 110 [own translation]
5. Orozco Valladares. Orozco, Verdad Cronológica. 29
6. Orozco, José Clemente. Autobiografía. 2a ed. Crónicas Series. México, D.F.: Ediciones Era, 1981. 15 [own translation]
7. Orozco Valladares. Orozco, Verdad Cronológica. 39
8. Reed. Orozco. 58 Orozco Valladares. Orozco, Verdad Cronológica. 103 [own translation]
9. Orozco Valladares. Orozco, Verdad Cronológica. 103 [own translation]
10. Reed. Orozco. 244-247
11. Orozco Valladares. Orozco, Verdad Cronológica. 545
12. Orozco Valladares. Orozco, Verdad Cronológica. 583
13. Orozco Valladares. Orozco, Verdad Cronológica. 571 [own translation]
14. Orozco Valladares. Orozco, Verdad Cronológica. 441
15. Paz, Octavio. México En La Obra De Octavio Paz. Vol. III. Los privilegios de la vista. México, D.F.: Fondo de Cultura Económica, 1987. 318 [own translation]
16. Loos, Adolf. “Ornament and Crime.” Paperback, no. 7 (2011). 2 [own translation]
17. “José Clemente Orozco.” Museo de Arte Carrillo Gil. Secretaría de Cultura. http://www.museodeartecarrillogil.com/coleccion/artistas-de-la-coleccion/jose-clemente-orozco. http://www.museodeartecarrillogil.com/coleccion/artistas-de-la-coleccion/jose-clemente-orozco.
18. Reed, Alma M. Orozco. 243
19. Orozco. Autobiografía. 100
20. Hambidge, Jay. The Elements of Dynamic Symmetry. Nueva York: Dover Publications, 1967. XI
21. Orozco. Autobiografía. 103
22. Fletcher, Rachel. “Dynamic Root Rectangles Part One: The Fundamentals.” Nexus Network Journal 9.2 (2007): 1
23. Hambidge. The Elements of Dynamic Symmetry. 17
24. Orozco. Autobiografía. 104 [own translation]
25. Ando, Tadao, et al. Luis Barragán: La Revolución Callada. Edited by Federica Zanco. Milano: Skira, 2001. [own translation]
26. Orozco, Clemente. “José Clemente Orozco. Mexican Pueblo. 1929: MoMA.” The Museum of Modern Art. Accesed on November 1, 2019. https://www.moma.org/collection/works/77130
27. Hambidge. The Elements of Dynamic Symmetry. 18
28. Hambidge. The Elements of Dynamic Symmetry. 33
29. Hambidge. The Elements of Dynamic Symmetry. XV
30. Hambidge. The Elements of Dynamic Symmetry. 17
31. Orozco, José Clemente. Cuadernos. Organized by Raquel Tibol. Ciudad de México: Cultura, SEP, 1983. 9
32. Orozco. Cuadernos. 248
33. Orozco. Cuadernos. 107
34. Orozco. Cuadernos. 102
35. Orozco. Cuadernos. 103
36. Orozco. Cuadernos. 106
37. Hambidge. The Elements of Dynamic Symmetry. 105-109
38. Hambidge. The Elements of Dynamic Symmetry. 28-29